The VRP-2 dynamics, with the parameter alpha value approaching the value equal to the value of the dimensionless fine-structure constant, features maximum variety with regard to the number of bifurcations with the minimum degree of chaosticity.
D. B. Volov Specific behavior of one chaotic dynamics near the fine-structure constant http://arxiv.org/abs/1205.6091
http://chaosandcorrelation.org/Chaos/DV_1_5_2012.pdf
http://www.sciteclibrary.ru/rus/catalog/pages/11612.html
This files contains an articles describing the Verhulst-Ricker-Planck dynamic and its relation to the fine structure constant.
The MathCAD's text program for the bifurcation diagram "four rats" (D.B.Volov, Russia, Samara).

Source code in MATLAB to reproduce the bifurcation diagram "four rats" (A.P.Trounev, Toronto, Canada)
(smile must be replaced by a colon)
x(i+1)=-L(k)/(x(i)^2(exp(x(i))+alpha))
L=zeros(1,500);
y=zeros(1,128);
ly=zeros(1,128);
alpha=1/137.035999074;
dL=(3.7+exp(1.1989))/500;
for k=1:length(L)
for i=1:length(y)
if (k==1)
L(k)=-3.8;
y(k, =1;
=1;
ly(k, =log(y(k,
=log(y(k, );
);
else
if (i==1)
L(k)=L(k-1)+dL;
V=y(k-1,128)*y(k-1,128)*(exp(-y(k-1,128))+alpha);
y(k,i)=exp(L(k))/V;
ly(k,i)=log(y(k,i));
else
V1=y(k,i-1)*y(k,i-1)*(exp(-y(k,i-1))+alpha);
y(k,i)=exp(L(k))/V1;
ly(k,i)=log(y(k,i));
end
end
end
end
for i=1:128
plot(L,ly(:,i),'.k')
hold on
title('a=1/137');
xlabel('lnK');ylabel('lnx');
end
The result:
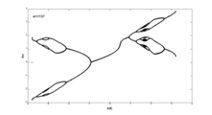 The bifurcation diagram "four rats" one-dimensional dynamic.
The bifurcation diagram "four rats" one-dimensional dynamic.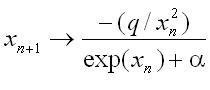
Code for the Wolfram Mathematica 8 & result (A.P.Trounev, Toronto, Canada):
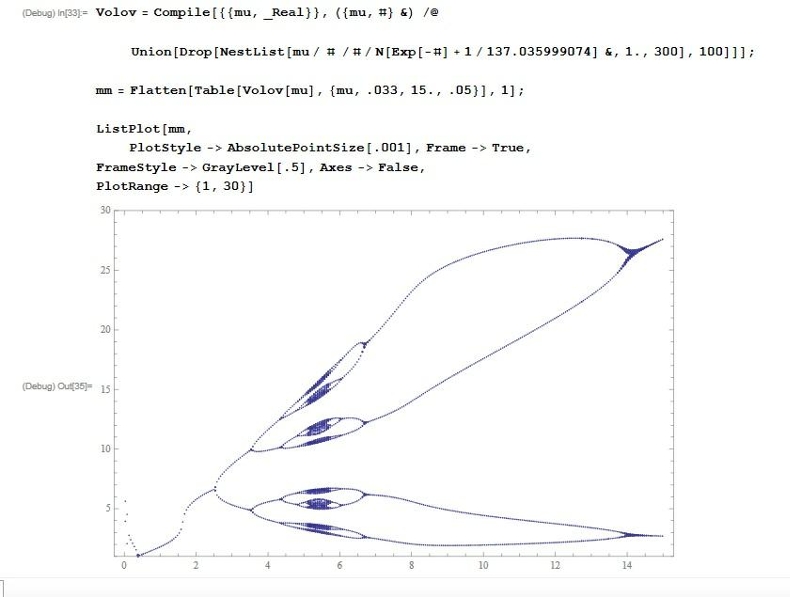
Nonlinear Phenomena.
1. Elsevier
Physica D (Nonlinear Phenomena)
Communications in Nonlinear Science and Numerical Simulation
International Journal of Non-Linear Mechanics
2. Physical Review E
3. Chaos
4. Ergodic Theory and Dynamical Systems
5. Journal of Dynamics and Differential Equations
6. International Journal of Bifurcation and Chaos (IJBC) in Applied Sciences and Engineering

